Polar Home

 Even-Mode Impedanz — eine Einführung.

Nicht alle Signale auf einem gekoppelten Leitungspaar sind jedoch differentiell. Das einfachste Beispiel ist elektrisches Rauschen. Ein Grund für den Einsatz differentieller Leitungen ist die Eigenschaft, Signale mit kleiner Amplitude selbst in Gegenwart eines starken Rauschsignals unverzerrt an der Empfangsstelle zu rekonstruieren. Da die beiden Leiter eng aneinander liegen, werden sie dem gleichen Störfeld ausgesetzt. diese induziert Rauschen in beiden Leitungen mit gleicher Amplitude und Polarität. Während das Originalsignal entgegengesetzte Polarität aufweist und daher dem Einfluss der virtuellen Masse ausgesetzt ist, wird das Rauschsignal diesen Einfluss nicht erfahren. Tatsächlich wird das Rauschsignal aufgrund der identischen Signalform eine höhere Impedanz auf beiden Leitungen erfahren. Die Impedanz, welche das Rauschsignal während der Ausbreitung erfährt ist daher die Even-Mode Impedanz.

Definitionen der Impedanzbegriffe:

Single ended Zo: Die gemessene Impedanz einer einzelnen Leitung, welche nicht mit einer zweiten benachbarten Leitung gekoppelt ist.

Differential (Zdiff): Die gemessene Impedanz zwischen einem Leitungspaar, wenn beide Leitungen mit identischer, jedoch entgegengesetzter Amplitude (Gegentaktsignal) angesteuert werden. (Zdiff entspricht dem doppelten Wert der Odd-Mode Impedanz)

Odd Mode (Zoo): Die Impedanz einer Leitung eines Leitungspaares, wenn die zweite Leitung mit identischer, jedoch entgegengesetzter Amplitude (Gegentaktsignal) angesteuert wird. (Zoo entspricht dem halben Wert der differentiellen Impedanz.)

Common mode (Zcm): Die gemessene Impedanz eines Leitungspaares, wenn beide Leitungen mit einem identischen (Gleichtakt-) Signal angesteuert werden.

Even mode (Zoe): Die Impedanz einer Leitung, wenn beide Leitungen einers Leitungspaars mit einem identischen (Gleichtakt-) Signal angesteuert werden. (Zoe entspricht dem doppelten Wert der Common-Mode Impedanz.

Ja, es gibt eine dritte Lösung. Diese ist elegant und möglicherweise nicht in jedem Fall erforderlich. Bei dieser Methode werden zuerst die Odd- und Even-Mode Impedanz terminiert. Zuerst werden die beiden Leitungen mit dem korrekten Even-Mode Wert gegen Masse abgeschlossen (wir nennen diese beiden Widerstände Ra und Rb). Dann wird ein zusätzlicher Widerstand Rc zwischen das Leitungspaar eingefügt..   

Abb. 2a Typischer Pi-Abschluss eines gekoppelten Leitungspaars

Dieser Widerstand Rc ist für das Even-Mode Signal nicht wirksam, da der Even-Mode anteil in beiden Leitungen identisch ist und kein Even-Mode Strom durch den Widerstand fließt. 

Abb. 2b Äquivalente Terminierung (mit Rc als Unterbrechung) im Even-Mode Betrieb

Im Odd-Mode Betrieb liegt das Zentrum des Widerstands Rc immer auf 0V. Dieser Widerstand (Rc/2) liegt nun parallelgeschaltet mit dem Even-Mode Abschlusswiderstand. Die Odd-Mode Impedanz entspricht daher der Parallelschaltung von ½ Rc mit Ra.

Abb. 2c Äquivalente Terminierung (mit virtueller Masse) im Odd-Mode Betrieb

 Diese Anordnung bietet eine perfekte Terminierung des Signals sowohl im Even- als auch im Odd-Mode Betrieb.

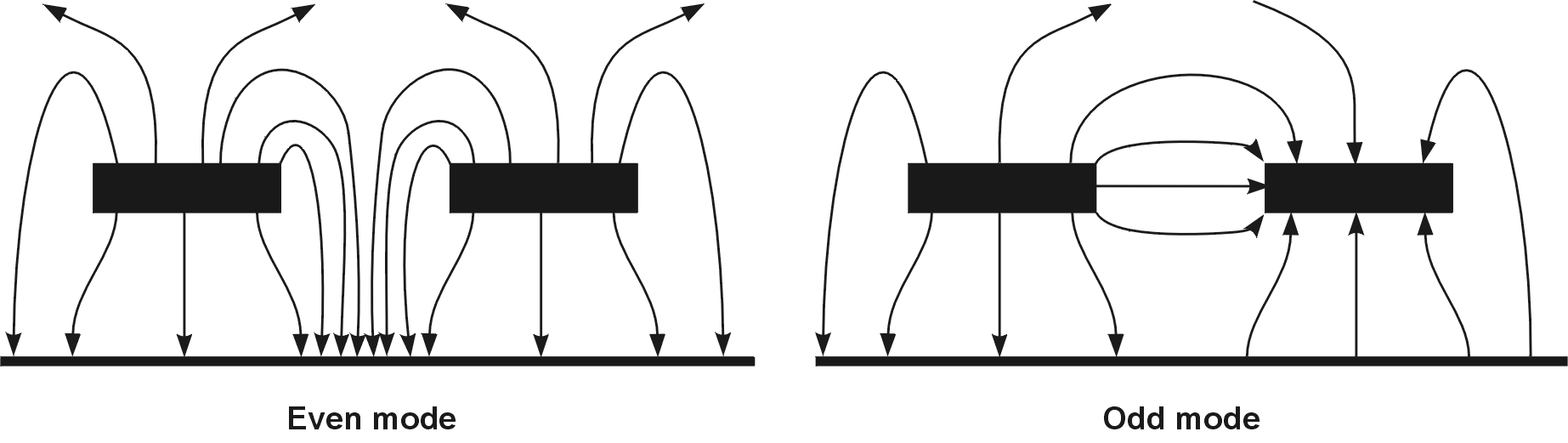
Abb. 4a Elektrische Felder im Even- und Odd-Mode

Abb. 4b Magnetische Felder im Even- und Odd-Mode

Im Odd-Mode erzeugt die entgegengesetzte Polarität der Signale eine "virtuelle" Masselage zwischen den beiden Leiterbahnen.  

Abb. 4c Virtuelle Masse zwischen den Leitungen im Odd-Mode

Eine steigende Zahl von Anwendungen (z.B. USB 2.0) fordert die Definition der Odd- und Even-Mode Impedanz. Dies bedeutet, dass grösseres Augenmerk auf die Datenaufbereitung der impedanzkontrollierten Leiterplatten gelegt werden muss. Es ist wichtig, das kleinere Änderungen der differentiellen Impedanz zu keinen Toleranzüberschreitungen der Even- oder Odd-Mode Impedanz führen. Die Polar Instruments Si6000c Software setzt leistungsfähige 2D Field Solver ein, um sowohl die Odd- als auch die Even-Mode Impedanz zu berechnen. Diese kann sowohl rasch in der Quicksolver-Oberfläche als auch in Microsoft Excel für eine detailliertere Analyse des Zusammenhangs zwischen Geometrie und Even/Odd Mode berechnet werden. (siehe Abbildung 5 unten).   

Abb. 5 Odd- und Even-Mode Impedanz über der Leiterbahn-Separation.

Weitere Informationen zum Thema Berechnung und Messung impedanzkontrollierter Leiterplatten erhalten Sie unter hermann.reischer@polarinstruments.com.

Detailliertere Informationen finden Sie auch in folgender Fachliteratur:

Hall, Hall, McCall, High-speed Digital Design, Wiley, 2000
Howard Johnson and Martin Graham, High Speed digital design: A handbook of Black Magic, Prentice Hall 1993.